A számoláshoz az első segédeszközt a kéz ujjai jelentették. Ezért volt “kézenfekvő” a tízes számrendszer használata. Később köveket, fadarabkákat is használtak a számolás segítésére alkalmi eszközként.
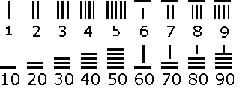
Ezután jelentek meg a már kimondottan számolás céljára készített, megmunkált, tartós használatra szánt kövek és pálcikák. A számolópálcák használatának az i.e. V. sz.-ból is van nyoma Kínában. Koreában még a XX. sz. elején is ilyen pálcikákkal tanították a gyerekeket számolni. Az ábrán látható régi kínai ún. pálcikaszámjegyek világosan magukon viselik a számolópálcák használatának nyomát.
A vonalak jelentették az 1-es, 10-es, 100-as, stb. helyiértékeket, a köztük lévő hézag pedig az 5-öt, 50-et, 500-at, stb. A számokat kavicsokból rakták ki, mindegyik helyiértékre a megfelelő számú kavicsot. Használtak ilyen célra porral borított táblát is.
Ezt a fajta vonalas abakuszt használták szerte Európában a római számokkal való számolás idején. Az eredményt igen könnyű volt leírni római számokkal. A későbbi időkben is előfordul, elsősorban a kevésbé képzett emberek körében (éppen ezért “paraszt számvetésnek” is nevezték).
A görögök, perzsák, rómaiak már állandó eszközt, bevésett vonalakat vagy csatornákat tartalmazó táblákat és ugyancsak állandó, a táblához illó méretű köveket használtak a számoláshoz. A kavics latin neve calculus. Ugye nem nehéz ráismerni kalkulátor szó ősére?
Néhány kép különböző abakuszokról:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |
3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | |
4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | |
5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | |
7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | |
8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | |
9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | |
10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |
1623-ban Wilhelm Schikard (1592-1635) tübingeni professzor a négy alapművelet elvégzésére alkalmas számológépet készített. A gép elkészítésére a késztetést valószínűleg a Keplerrel folytatott beszélgetései jelentették. A gépről is csak Kepler iratai között maradt egy vázlat. Az eredeti gép a harmincéves háborúban eltűnt, a Kepler számára készített másodpéldány még a műhelyben elégett, Schikard pedig egész családjával együtt meghalt pestisben, mielőtt még egyet készíthetett volna. 
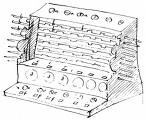
A vázlat alapján 1960-ban sikerült egy jól működő rekonstrukciót készíteni. A számológép felső része hat darab függőlegesen elrendezett, hengeres pálcát tartalmaz, így legfeljebb hatjegyű számokkal való műveletvégzésre alkalmas. Az egyes számjegyeket a pálcák megfelelő elforgatásával lehet beállítani. A pálcák alatt fogaskerekekből készített számlálómű található. A felhasználónak a pálcákról leolvasott részeredményeket kézzel kellett bevinni a számlálóműbe és azzal összeadni. A végeredmény a gép alján lévő kis nyílásokban jelent meg. Schikard külön számtárcsákat is felszerelt a gépre, amelyek megfelelő elforgatásával a legfeljebb hatjegyű részeredményeket lehetett tárolni, megkímélve ezáltal a felhasználót a leírástól. A gép jelezte a túlcsordulást is: ha a hetedik helyiértékre is szükség lett volna, megszólalt egy csengő.
