Számítástechnika története
dióhéjban:
néhány fontos történeti elem
a teljesség igénye nélkül
A számítógépeket fejlődésük szempontjából számítógép-generációkba sorolják.
Ez a besorolás viszont nem köthető pontos évszámokhoz, a különböző források más és más éveket adnak meg. Sokkal jellemzőbb az egy generációra, hogy az akkor készült gépeknek mi volt a fő építőeleme:
1. generáció: elektroncsövek
2. generáció: tranzisztorok
3. generáció: integrált áramkörök (chip-ek)
4. generáció: nagy bonyolultságú integrált áramkörök (mikrochip-ek)
Érdemes a youtube-on rákeresni videókra, amelyek a számítógépek kialakulásáról, működéséről szólnak, illetve feltalálóikról.
Tipp: írd be a keresőmezőbe egy-egy számítógép, feltaláló, vagy számítógépes cég nevét, máris rengeteg érdekesség között válogathatsz!
2010.05.01. 12:58
Neumann Jánost a modern számítógép atyjának tekinthetjük. Elvei alapján működnek mai számítógépeink is. Neumann több más amerikai magyar emigráns tudóssal is együtt dolgozott, akik szintén szerepet vállaltak a számítástechnika fejlődésében.A Neumann-elvek
A ma használt számítógépek felépítését, működését nagyban meghatározta Neumann János munkássága. 1946-ban a „First Draft of a Report on the EDVAC by John von Neumann című jelentésében fogalmazta meg azokat az elveket, amelyek alapján a mai számítógépek is felépülnek. Ezek az elvek röviden a következők [5]:
1. A számítógép legyen teljesen elektronikus, külön vezérlő és végrehajtó egységgel rendelkezzen.
2. Kettes számrendszert használjon.
3. Az adatok és a programok ugyanabban a belső tárban, a memóriában legyenek.
4. A számítógép legyen univerzális.
5. Folyamatos emberi beavatkozás nélkül hajtsa végre a műveletsort, logikai döntéseket hozva feldolgozás közben.
Kemény János (1926-1992), a Dartmouth Kollégium rektoraként kötelezővé tette a számítógépek (terminálok) használatát a bölcsész és jogi karon is, és e célból megalkotta az elvont gépi programozás helyett a BASIC nyelvet (Beginner’s All-purpose Symbolic Instruction Code = a kezdők bármely célra használható szimbolikus utasítás kódja). Szintén Kemény János nevéhez fűződik az osztott idejű számítógép hálózat is, melyet az IBM első Robinson-díja ismert el.
Munkájában a fizikus Szilárd Leó közreműködött, ő vezette be az információ elemi kvantumát (igen/nem), amit ma a bit néven ismerünk. 
Megemlítendő még a Time hetilap által 1997-ben az év emberének nevezett Andrew Grove (Gróf András) is, aki az INTEL vezéreként évente megtöbbszörözte a mikroprocesszorok sebességét.
Az érdeklődők számára ajánlom
DR. RAFFAI MÁRIA: A hazai számítástechnika története informatikatörténeti szakkönyvét, amely elérhető .pdf formátumban az interneten is!
Valamint:
+ egy kis érdekesség: Az első magyarországi számítógép
Magyarországi vonatkozása is van a számítógépkutatásnak. 1956 nyarán a Kibernetikai Kutatócsoport (KKCS) létrehozta az M3-at, ez volt az első magyar számítógép. A végleges változat csak 1959-re készült el. S hogy mire is lehetett használni ezt a szerkezetet? Például tervhivatali mátrixokat számolt ki, bonyolult matematikai és nyelvészeti problémákat oldott meg, és az épülő Erzsébet híd statikai számításainak az ellenőrzését is el tudta végezni.
Az M3 tárolásához egy kb. 60 m2-es teremre volt szükség, amelyben egy ventilátor gondoskodott a hűtésről. A teremben nagyon meleg volt, hiszen a több száz elektroncső pillanatok alatt befűtötte a termet. A programozás kezdetekben rendkívül nagy nehézséget jelentett, hiszen a programozók is tapasztalatlanok voltak, így ha valahol elakadt a program, akkor a futtatást elölről kellett kezdeni, ami a sebessége mellett nem is jelentett olyan kicsi időveszteséget. Az input-output információkat telexszalag segítségével oldották meg. A gép nyolcas számrendszerben működött, az eredmények is ebben a számrendszerben jelentek meg. Az M3 operációs rendszer nélküli gép volt. A programozása gépi kódban történt. A memóriája 1024 szavas, 31 bites szavakból állt.
Érdekesség: Az M3 költsége csak töredéke volt az Egyesült Államokban ekkoriban használt UNIVAC számítógépekének.
+ még egy (mert befejezni nem lehet, csak abbahagyni...)
Roska Tamás és a látócsip
A Roska Tamás akadémikus vezette kutatócsoport több, mint tízévi, amerikai-spanyol együttműködésben végzett munka eredményeként a jelenleg alkalmazott számítógépek működési elvétől gyökeresen eltérő konstrukcióval dolgozó analogikai számítógépet fejlesztett ki. Az elnevezés az analóg és a logikai működés egyesítésére utal. Roska Tamás szerint a digitális technika ismert fizikai alapjainak és működési módjainak átgondolása igencsak időszerű volt. Az optikai érzékelők - így például a kamerák - ontják az analóg jeleket, ezek digitálisra konvertálása pedig nem megy olyan könnyen, lassú és energiaigényes folyamat. „Azokon a területeken - mondja Roska -, ahol változó jelek tömegével kell dolgozni, olyan számítógép válhat be, amelyben közel kerül egymáshoz az érzékelés és a feldolgozás.”
Az analóg módon működő és logikai műveletekre képes komputer, az analogikai számítógép lelkét, a CNN csipet Leon Chua, a Berkeleybeli University of California kínai származású amerikai professzora és tanítványa, L. Yang találta fel 1988-ban. A CNN egy Cellurális Neurális/Nemlineáris hálózat. Olyan processzorsereg, amelyben az egyes processzorok (cellák) egy négyzetrács csúcspontjaiban foglalnak helyet. Mindegyik cella a közvetlen környezetében lévővel van összeköttetésben, azoktól hatást kap, illetve azokra hat. Ezek a hatások alakítják ki a CNN működését. Erre építve 1992-ben Roska és Chua megalkotta az úgynevezett CNN Univerzális Gépet, amely egy kétdimenziós rácson több ezer CNN elemi processzort tartalmaz. A CNN csip maga egy vizuális mikroprocesszor, amelyben minden egyes tranzisztor fényérzékelő optikával rendelkezik.
Az analogikai számítógépben a jelek folytonosak, érzékszerveinkből mintegy hullámszerűen terjednek tovább az idegrendszerben. Ezért a tudósok ezt a modellt hullámszámítógépnek is hívják. Egy új számítógépfajta jelent meg: vizuális mikroprocesszorként (látócsipként) már működő példányokat is lehet vásárolni. A számítógép alapelvét agykutatók, Hámori József, Frank Werblin és mások munkái inspirációjára alkotta meg Roska Tamás és Leon Chua. Ma már megszületett az új retinamodellnek a vizuális mikroprocesszoron történő részleges megvalósítása is, Bálya Dávid fiatal magyar kutató jóvoltából.
2002. március 2-án a Bolyai-díjat RoskaTamás vehette át Mádl Ferenc köztársasági elnöktől.
2010.05.01. 12:32
Az ötödik generációs számítógépek fejlesztése napjainkban is folyamatban van, ezek egyes feladatokat úgy látnak el, mintha ember végezné azokat.
Sokféle irányban folyik kutatás, lássunk néhány példát!
· Az egyik jelenlévő trend a számítógépek fejlesztésében a mikrominiatürizálás, az az igyekezet, hogy mind több áramköri elemet sűrítsenek mind kisebb és kisebb méretű chipekbe.
· A kutatók az áramkörök sebességét a szupravezetés felhasználásával is igyekeznek felgyorsítani.
· Szintén aktívan kutatott terület a párhuzamos feldolgozás, azaz amikor sok áramkör egyidejűleg különböző feladatokat old meg. A párhuzamos feldolgozás alkalmas lehet akár az emberi gondolkodásra jellemző komplex visszacsatolás utánzására is.
· Fontos út a számítógépes hálózatok fejlődése. Ezekben a hálózatokban már műholdakat is felhasználnak a számítógépek világhálózatának működtetésére.
· Folynak kutatások az optikai számítógépek kifejlesztésére is. Ezekben nem elektromos, hanem sokkal gyorsabb fényimpulzusok hordoznák az információt.
· Olyan gépek létrehozására irányuló kutatás, amelyek már komplex problémákat tudnának alkotó módon megoldani. Ennek a fejlesztésnek a végső célja az igazi mesterséges intelligencia létrehozása lenne.
Japánban egy 1981 októberében tartott konferencián jelentettek be egy új állami kutatási tervet. A japán kormány 1982 áprilisában megalakította az Institute for New Generation Computer Technology (ICOT) nevű intézményt a számítástechnikai kutatások végzésére, egész pontosan az FGCS (Fifth Generation Computer Systems) projekt vezetésére. Sok ezer mérnököt foglalkoztattak Tokió külvárosában a munkán. Ennek az új – szerintük az ötödik – generációnak fontos alkotórésze lesz a mesterséges intelligencia, a szakértői rendszerek, a szimbólumokkal való műveletvégzés. Intelligens számítógép létrehozása a cél, amelyik lát, hall, beszél és gondolkodik. Képes asszociálni, tanulni, következtetéseket levonni és dönteni.
A japánok a munkát 10 évre tervezték. Cél: olcsó személyi munkaállomás kidolgozása, ami több ezer objektumból és több ezer szabályból álló tudásbázist tud kezelni, másodpercenként mintegy egymillió logikai következtetést tud levonni.
Az eredményt az 1990-es évek elejére várták: egy olyan gépet, amelynek a tudása több tízezer következtetési szabályt és több százmillió objektumot foglal magába (ez utóbbi nagyjából az Encyclopaedia Britannica ismeretanyaga), megérti a köznapi nyelven beszélt és írott szöveget és értelmezni tudja a grafikus adatbevitelt.
A kezdeti lépések bár biztatóak, az emberi gondolkodással, érzékeléssel kapcsolatos kutatások azonban azt mutatják, hogy az elkövetkezendő 10 évben még nem számíthatunk a látó, halló, beszélő, gondolkodó intelligens számítógépre.
Japánban egy 1981 októberében tartott konferencián jelentettek be egy új állami kutatási tervet. A japán kormány 1982 áprilisában megalakította az Institute for New Generation Computer Technology (ICOT) nevű intézményt a számítástechnikai kutatások végzésére, egész pontosan az FGCS (Fifth Generation Computer Systems) projekt vezetésére. Sok ezer mérnököt foglalkoztattak Tokió külvárosában a munkán. Ennek az új – szerintük az ötödik – generációnak fontos alkotórésze lesz a mesterséges intelligencia, a szakértői rendszerek, a szimbólumokkal való műveletvégzés. Intelligens számítógép létrehozása a cél, amelyik lát, hall, beszél és gondolkodik. Képes asszociálni, tanulni, következtetéseket levonni és dönteni.
A japánok a munkát 10 évre tervezték. Cél: olcsó személyi munkaállomás kidolgozása, ami több ezer objektumból és több ezer szabályból álló tudásbázist tud kezelni, másodpercenként mintegy egymillió logikai következtetést tud levonni.
Az eredményt az 1990-es évek elejére várták: egy olyan gépet, amelynek a tudása több tízezer következtetési szabályt és több százmillió objektumot foglal magába (ez utóbbi nagyjából az Encyclopaedia Britannica ismeretanyaga), megérti a köznapi nyelven beszélt és írott szöveget és értelmezni tudja a grafikus adatbevitelt.
A kezdeti lépések bár biztatóak, az emberi gondolkodással, érzékeléssel kapcsolatos kutatások azonban azt mutatják, hogy az elkövetkezendő 10 évben még nem számíthatunk a látó, halló, beszélő, gondolkodó intelligens számítógépre.
2010.05.01. 11:57
Az 1970-es évek közepe óta számíthatjuk az idejét és a mai napig tart. A gépek igen nagy integráltságú (VLSI, Very Large Scale Integration) áramkörökből épülnek fel.
Általánossá válik a félvezetős, integrált áramkörökből készült memória is.
Az új technológiának köszönhetően tovább csökken a hardver ára, egy számítógéprendszer árának már akár 75%-a is lehet a szoftver.
A távadatátvitel lehetővé teszi gyakorlatilag bármelyik két gép összekapcsolását és napjainkra már szinte mindegyik számítógép kapcsolódik valamilyen hálózathoz.
Megjelenik a mikroprocesszor, majd ezt felhasználva rohamosan elterjed a személyi számítógép. Általánossá válik használatuk szövegszerkesztésre, táblázatkezelésre, grafikára, adatbáziskezelésre, stb.
Az operatív tár mérete jelentősen nő: egy közepes második generációs gép (IBM 1401) memóriájának mérete jellemzően 4 és 16 kbájt között volt, a negyedik generációs IBM 4341-nek már ezerszer akkora, 4-16 Mbájt volt a memóriája.
A korszak fontosabb eseményei
1970-ben jelentik be az IBM System/370-es gépcsaládot, ami meghatározó volt a negyedik generáció elején. A család elnevezésében a 70 a hetvenes évekre utal. A gépcsalád népszerűségére jellemző, hogy más gyártók is építettek velük kompatibilis számítógépeket.
Az első mikroprocesszor, az egyetlen IC-ben realizált processzor 1971-ben készült. Ted Hoff, a Stanford University mérnöke tervezte. Az Intel készítette, egy 7 mm oldalhosszúságú négyzet alakú szilíciumlapkán 2300 tranzisztort tartalmazott.
1972-ben megjelennek az első tudományos célú zsebszámológépek.1974-ben forgalomba kerül az első programozható zsebszámológép, a Hewlett-Packard által gyártott .
1974-ben megjelenik az első személyi számítógép, az Altair 8800.Magát a gépet eredetileg mint alkatrészt adták el, de némi plusz pénzért teljes értékű gépet lehetett belőle összeállítani. Habár nem volt billentyűzete, de "programozni" az előlapi kapcsolókkal lehetett - és mivel nem volt videó-kimenete (sem), az eredményt LED-diódákra adta ki.
1974-ben a Stanford Egyetemen üzembe helyezik a számítógépes orvosi diagnosztikai rendszert.
1976-ban üzembe helyezik az első Cray-1 szuperszámítógépet.
Az 1970-es években jelenik meg az interaktív számítógépes tervezés.
1979-ben készült el a VisiCalc, az első táblázatkezelő program.
1981-ben jelenik meg az IBM PC, aminek leszármazottai mai életünk meghatározó elemei. (PC = Personal Computer, azaz személyi számítógép.)
A Time magazin évente kitüntet valakit, aki az adott évben előre vitte valamiben a világot. 1982-ben a számítógép kapta a “Man of the Year” címet.
Jellemző gépkategóriák az 1980-as évek közepén:
- Szuperszámítógép: legismertebb típus a CYBER és a Cray. A Cray a kiépítéstől függően akár 20 millió dollárba is kerülhet. Speciális födém kell alá, hogy elbírja a súlyát. A vételi ár tartalmazza két teljes munkaidőben foglalkoztatott karbantartó mérnök díját is a gép egész élettartamára. Az installált szupeszámítógépek száma nem éri el ekkor még a 150-et.
- Nagyszámítógép (mainframe): nagy cégeknél (bankok, kereskedő és gyártó cégek, kormányhivatalok) ezek végzik az adatfeldolgozás zömét. A jellemző áruk 400.000 és 1.000.000 dollár között volt. Üzemeltetésük klimatizált helyiségben történik.
- Miniszámítógép: kisebbek, lassabbak és olcsóbbak a nagygépeknél. Nincs különleges környezeti működési feltételük, az iroda sarkában is állhatnak. Jellemző áruk 20.000-40.000 dollár volt.
- Mikroszámítógép: mikroprocesszort használ. Személyi számítógépnek is nevezik. Nagygépre kötve lehetővé teszik a munka megosztását a nagygép és a mikrogép között. Vannak hordozható gépek is. A méret csökkentésének a billentyűzet és a képernyő használható méreten tartása szab korlátot.
A Cray szuperszámítógép
Seymour Cray eredetileg a CDC-nél (Control Data Corporation) dolgozott szuperszámítógépek fejlesztésén. 1972-ben megalapította saját cégét, a Cray Research-öt.Az első általa tervezett szuperszámítógép, a Cray-1 1976-ban került kereskedelmi forgalomba. Mintegy hétmillió dollárba került, csak kormányhivatalok és igen nagy cégek tudták megvenni.
Ez volt az első olyan számítógép, amely képes volt másodpercenként több mint százmillió műveletet végrehajtani. Az alapműveletek végrehajtási ideje 12,5 ns.
A sok megoldandó technológiai probléma közül ez egyik legfontosabb az volt, hogy hogyan vezessék el a nagysebességű áramkörök által termelt hőt. Ezt úgy oldották meg, hogy az áramköröket freonnal hűtött függőleges lapokra szerelték.
Azóta építettek ugyan gyorsabb számítógépeket is, de a Cray-1-et azóta is használják összetett problémák matematikai tanulmányozására (ilyen problémák például a beszédfelismerés, az időjárás előrejelzése, valamint a fizikai és a kémia alapkérdései).
A Cray-1 a teljesítmény nem hivatalos mértékegységeként is nyomot hagy maga után: néhány új szuperszámítógépet 1000 Cray teljesítményűre terveznek.Az imponáló teljesítményadatok ellenére mindennapjaink meghatározó számítástechnikai tényezői mégsem az egyre tökéletesebb szuperszámítógépek, hanem az ellenkező véglet, a személyi számítógépek.
A személyi számítógépek megjelenése
1974-ben egy kis cég New Mexico-ban piacra dobta az Altair 8800 nevű személyi számítógépet egy összeszereletlen készlet formájában. A készlet nem egészen 400 dollárba került. Az információ bevitelére a gépnek nem billentyűzete volt, hanem csak egy kapcsolótáblája. Ez volt az első, kimondottan személyes felhasználásra tervezett asztali számítógép. Igaz ugyan, hogy az Altair kapacitása 1%-a sem volt a Hewlett-Packard 1991-ben kiadott, egy tenyérben elférő számítógépének, de ez a gép indította el a számítógépes elektronika máig tartó forradalmát.
A mikroszámítógép-készlet iránt hirtelen olyan nagy kereslet alakult ki, amire senki sem számított. Számtalan kis cég alakult az új piac igényeinek kielégítésére. Az első nagyobb elektronikai cég, amely belekezdett személyi számítógépek gyártásába és árusításába, a Tandy Corporation volt. Ők 1977-ben kezdték árusítani számítógépüket, amellyel hamarosan uralkodóvá váltak a piacon. Gépüknek két vonzó tulajdonsága volt: egy billentyűzet és egy katódsugárcsöves monitor. A gép népszerűségéhez az is hozzájárult, hogy programozni lehetett és a felhasználó mágneskazettákon tárolni tudta az információt.
Sok hardvergyártó kezdett ezután kész személyi számítógépeket árulni, a szoftverfejlesztők pedig olyan programok készítésébe fogtak, amelyekkel ezek a számítógépek alkalmasak voltak szövegszerkesztésre, adatfeldolgozásra és rajzolásra.
Két mérnök-programozó (Stephen Wozniak és Steven Jobs) Apple Computers néven alapított egy számítógépgyártó céget.
Az első Apple számítógépet 1977-ben adták el. A számítógépeiken alkalmazott újítások között volt a kiterjesztett memória, az adatok és programok tárolására szolgáló olcsó lemezmeghajtó és a színes grafika.(!) Az Apple lett az Egyesült Államok történelmének leggyorsabban növekvő cége. Az ő sikerük is sokaknak ösztönzést jelentett, hogy ezen a területen próbálkozzanak. Az évtized végére a személyi számítógépes piac teljesen kialakult.1979-ben jelent meg a VisiCalc, az első táblázatkezelő program. Ezzel már a programozásban gyakorlatilag teljesen járatlan emberek is komoly és összetett problémák megoldására tudták a számítógépet használni. Igen fontos tényező volt a mikroszámítógépek robbanásszerű elterjedésében.
1981-ben az IBM piacra dobta saját mikroszámítógépét, az IBM PC-t. Bár nem használta fel a legújabb technológiákat, a PC mérföldkővé vált a számítástechnikában. Bebizonyította, hogy a mikroszámítógép nemcsak egy divatos irányzat, hanem az üzleti élet szükséges eszköze. További érdeme, hogy olyan operációs rendszert használt (DOS), amely hozzáférhető volt a többi számítógépgyártó cég számára is, és így a piac szabványosodásához vezetett.
Ugyancsak 1981-ben készítette el Adam Osborne az első hordozható mikroszámítógépet, az Osborne 1-et.
A gép súlya kb. 11 kg volt, a memóriája 64 kB kapacitású és 1.795 dollárért árulták.A személyi számítógép olyan olcsó, hogy egy magánszemély is könnyűszerrel megveheti. Ráadásul minél többet vesznek belőle, annál olcsóbb, hiszen a nagy sorozatú gyártás minden termék árát leviszi. Beindult egy olyan folyamat, ami a mai napig tart: olcsóbban lehetett számítógépeket előállítani, ezért olyan helyeken is kifizetődő volt az alkalmazásuk, ahol korábban nem. Ezért sok számítógépet lehetett eladni, több mikroprocesszort kellett gyártani, így a számítógép még olcsóbb lett. Ezért még több helyen lehetett használni, ezért még többet gyártottak, ezért még olcsóbb lett, és így tovább.
A további fejlődés
Az 1980-as években a számítógépek rohamléptekkel váltak egyre kisebbé, jobbá és olcsóbbá. A nagyobb teljesítményű hardver összetettebb, könnyebben kezelhető programok készítését tette lehetővé. Ezért a számítógépek egyre gyorsabb processzorokkal, egyre nagyobb háttértárakkal és egyre nagyobb memóriával készültek.
Az egyik legkiemelkedőbb újítás az egyszerűbb, felhasználóbarát módszerek bevezetése volt amikroszámítógépek működésének vezérlésére. A hagyományos, parancsvezérlésű operációs rendszert felváltotta a grafikus felhasználói felület (graphical user interface, GUI). Az ilyen felületet használó gépeknél, mint pl. az Apple Macintoshnál (majd később a Windowst futtató IBM PC-knél) a felhasználónak csak egy ikont kell a képernyőről kiválasztani egy funkció végrehajtásához.
Ma már beszédvezérlésű gépek is léteznek: a felhasználó a köznapi beszéd szavaival, annak nyelvtani szabályai szerint beszélve adhat parancsot a számítógépnek.
1992-re a számítógépgyártás vált a világ leggyorsabban fejlődő iparágává.
1994-ben a világon mintegy 120 millió IBM-kompatibilis személyi számítógépet használnak. A fő felhasználó már nem az állami apparátus, hanem a magánszektor. 30 éve még az Egyesült Államok kormánya vásárolta meg az ország számítógép-termelésének 62%-át, ebben az évben már ez az arány nem éri el a 4%-ot. Bár ebben az évben az USA kormánya több mint 25 milliárd dollárt költ számítógépekre és számítástechnikai szolgáltatásokra, mégis csak 4 évente tudja lecserélni számítógépeit, szemben a magánszektorra jellemző 13 hónappal.
2010.05.01. 10:20
Az integrált áramkört (IC-t) 1958-ban fedezte fel Jack S. Kilby a Texas Instrumentsnél és Robert Noyce a Fairchild Semiconductornál. Ez az eszköz a harmadik generációs számítógépek jellegzetes építőeleme.
A tömegtermelés 1962-ben indult meg, az első integrált áramköröket tartalmazó számítógépek pedig 1964-ben kerültek kereskedelmi forgalomba.
A számítógépek több tevékenységet tudnak párhuzamosan végezni. Előrelépések történnek a távadatátvitelben.
Az integrált áramkörök tovább csökkentették a számítógépek árát, méretét és meghibásodási gyakoriságát. Ez tovább növelte a számítógépek iránti keresletet: az 1970-es évek elejére több mint 100.000 nagyszámítógépet és ugyancsak több mint 100.000 miniszámítógépet helyeztek üzembe. A harmadik generáció korszakát kb. az 1965-1971-es évekre lehet tenni.
Megjelenik a monitor és a billentyűzet, a lyukkártya kezd visszaszorulni.
Megjelennek az első valódi operációs rendszerek.
A miniszámítógépek tömeges előállítása 1960-as évek közepén kezdődik meg.
Mérföldkőnek számít a Gene Amdahl tervei szerint készült IBM System/360-as megjelenése 1965-ben (már 1964-ben bejelentették, de csak 1965-ben szállították először). 
Ez egy egész gépcsalád volt, amit eleve úgy terveztek, hogy a számítástechnikai teljesítmény széles skáláját átölelje. A család hat különböző teljesítményű modellből állt. Ezek egymással kompatibilisek voltak mind a hardver, mind a szoftver terén. Így megtehette azt egy cég, hogy a legolcsóbb olyan modellt vásárolja meg, ami éppen megfelelt pillanatnyi igényeinek, és később az igények növekedésével bővítette a memóriát, nagyobb teljesítményűre cserélte a gépet vagy még több perifériát adott hozzá. A már kész programjait azonban változatlanul használhatta az új gépen is, legfeljebb a futásidő és a memóriaigény változott.
Több szempontból is a korszak legnagyobb hatású számítógépe volt az IBM 360-as, sok jellegzetessége gyakorlatilag szabvánnyá vált a számítógépiparban.1969-ben ennél a gépcsaládnál választották szét először a hardvert és a szoftvert: külön tételként jelentek meg számlázáskor (ez tovább növelte a szoftver jelentőségét) és nem volt kötelező együtt megvásárolni őket. Ezt a politikát a többi cég is átvette. A számítógépek eladása nemcsak egy működő gép átadását jelentette ezután, hanem hardverből, szoftverből, oktatásból, karbantartásból, konzultációból álló komplex szolgáltatás értékesítését.
Széles körben elterjednek az igazi operációs rendszerek. A manchesteri egyetemen készített és 1961-ben üzem behelyezett ATLAS számítógép az egyik első olyan számítógép volt, aminek már igazi operációs rendszere volt.
szttort.blog.hu/media/file/A harmadik generációs számítógépek korszaka.ppt
2010.04.27. 21:09
A tranzisztort 1947-ben fedezte fel a Bell Laboratóriumban William Shockley, aki ezért aztán 1956-ban Nobel-díjat is kapott. A találmányt 1948-ban hozták nyilvánosságra. A tranzisztor tömeges alkalmazása a számítógépekben először az 1950-es évek végén történt meg.A tranzisztorokkal kisebb, gyorsabb és megbízhatóbb logikai áramköröket lehetett készíteni, mint az elektroncsövekkel. A második generációs számítógépek már másodpercenként egymillió műveletet is el tudtak végezni. A tranzisztorok sokkal kevesebb energiát fogyasztanak és sokkal hosszabb életűek. A gépek megbízhatósága kb. az 
ezerszeresére nőtt az első generációhoz képest. Kisebbek lettek az alkatrészek és kisebbek lettek az alkatrészek közötti hézagok is. Egyúttal sokkal olcsóbbá is váltak a számítógépek, emiatt nőtt az eladások száma: csak az IBM 1400-as sorozatból több mint 17.000 darabot helyeztek üzembe. Szaporodtak a számítógépgyártással foglalkozó cégek is. A második generáció korszakát kb. az 1959-1965-ös évekre lehet tenni.
ezerszeresére nőtt az első generációhoz képest. Kisebbek lettek az alkatrészek és kisebbek lettek az alkatrészek közötti hézagok is. Egyúttal sokkal olcsóbbá is váltak a számítógépek, emiatt nőtt az eladások száma: csak az IBM 1400-as sorozatból több mint 17.000 darabot helyeztek üzembe. Szaporodtak a számítógépgyártással foglalkozó cégek is. A második generáció korszakát kb. az 1959-1965-ös évekre lehet tenni.Az 1950-es évek közepén építették az első különlegesen nagy és különlegesen gyors számítógépeket, népszerű nevükön a szuperszámítógépeket.
Az elsők között volt a LARC és az IBM által készített Stretch. Ezeknél a gépeknél több olyan technikai megoldást vezettek be, amivel a számítógép tényleges sebességét növelni lehetett. Az egyik alapvető megoldás az egyidőben végrehajtható tevékenységek számának növelése volt. A legjelentősebb megoldást a párhuzamos feldolgozási technikák jelentették. A hardver eszközök felépítésénél uralkodóvá vált a moduláris felépítés, ami a karbantartást nagymértékben leegyszerűsítette.
A második generációtól kezdve számítógéprendszerről beszélhetünk, mert a memória mérete, a processzor típusa, a perifériák eltérők lehettek az egyes telepített gépek között, bár alapvetően ugyanarról az alapgépről volt szó.
A számítógépek üzemeltetésénél jellemző megoldás volt a kötegelt (batch) feldolgozás. A régi számítógépeknél minden egyes felhasználói programot külön futtattak, a számítógépet emberi beavatkozással állították meg a program futásának végén és előkészítették a következő program futtatásához. Ez a megoldás, illetve az emiatt fellépő veszteségidő az akkori gépek kis sebessége miatt nem okozott problémát.
A gépek sebességének növekedésével azonban felmerült a számítógép gazdaságosabb kihasználásának igénye, a feldolgozás egyes lépéseinek automatikus vezérlése. Ezt valósítja meg a programok kötegelt feldolgozásával a batch üzemmód. Általános megoldás volt, hogy egy egész sor programot előre mágnesszalagra írtak, a számítógép ezeket folyamatosan, egymás után feldolgozta és az eredményt egy másik mágnesszalagra írta.
A számítógépgyártók kezdtek rendszerprogramokat is adni a gépekhez, valamint olyan programokat, melyek a gyakori feladatok megoldására általánosan használható, úgynevezett utility programok, amikkel pl. fájlokat lehetett összefésülni, rendezni, másolni egyik tárolóeszközről a másikra, stb.
A gépek programozásban általánossá vált az akkoriban bevezetett magasszintű nyelvek (ALGOL, FORTRAN, COBOL) használata. Ez egyrészt a programozási munkát nagymértékben egyszerűsítette, másrészt természetesen megkövetelte a megfelelő fordítóprogramok meglétét.
A számítógép-rendszerekben egyre nőtt a szoftver értéke a hardverhez képest. Már ekkor voltak olyan rendszerek, ahol a szoftver ugyanannyiba került, mint a hardver.
Ugyancsak a második generáció idején kezdődött a cégek információs rendszerének számítógépesítése. A vezetőket olyan információkkal tudták így ellátni, ami növelte a profitot és elősegítette a cég irányítását.
A második generáció technikai jellegzetességeinek jó része már az elektroncsöves számítógépeknél megjelenik. Az 1955-ben gyártott csöves IBM 704 volt az első olyan üzleti számítógép, aminek volt egy “vezérlőprogramja”, egy kezdetleges operációs rendszer. Ennek a gépnek a későbbi modelljei és utója, az IBM 709-es már rendelkezett input-output processzorral, aminek kizárólagos feladata az adatbevitel-adatkivitel irányítása volt (akkoriban ezt a processzort adatszinkronizátornak, később csatornának hívták az IBM-nél). (Az IBM 7090 és a 7094 alapjában véve a 709-es tranzisztorizált változata volt és üzletileg igen sikeresnek bizonyult.)
2010.04.27. 20:44
Az elektroncsövet 1904-ben találták fel. Felfedezték hogy kapcsolóként is alkalmazható. Az elején azonban a csövek drágák, megbízhatatlanok és rövid életűek voltak, csak az 1940-es évektől használták őket számítógépek készítésére. Az elektroncsövek sokkal 
gyorsabb gépek építését tették lehetővé, mint a relék. Ennek az eszköznek a felhasználásával készült az első számítógép-generáció. Az első számítógép-generáció ideje nagyjából az 1946-1954 közötti évekre tehető.Általános jellemzők
Ebben a korban a gép szolgáltatásait egyszerre egy programozó használta. Így a lassú perifériákra való várakozás és a programozók egymás közti váltása alatt a processzor igen sokat tétlenkedett.Az első generációs gépek megbízhatóságára jellemző, hogy amikor az ENIAC üzembiztos működését bejelentették egy sajtóértekezleten, nagy büszkeséggel közölték, hogy volt már olyan 12 órás műszak, amelyben több órán keresztül működött hibamentesen a gép. Később is állandó műszaki felügyelet kellett e gépek működtetéséhez. A számítógép bármikor meghibásodhatott, a hiba megkereséséhez és kijavításához pedig hozzáértő szakemberek kellettek. A leggyakoribb hiba ok egy-egy cső kiégése volt. Ilyenkor azonban a sorozatban gyártott csövek paramétereinek nagy szórása miatt nem volt elég a kiégett csövet kicserélni, hanem azokat is cserélni kellett vele együtt, amikkel egy funkcionális egységet alkotott. A karbantartóknak már előre összemért csőkészletei voltak erre a célra.
ABC
Az Egyesült Államokban a Iowa State College-ban már 1939-ben megépítette egy elektronikus gép prototípusát John Atanasoff (1903-1995) és Clifford Berry (1918-1963) (Atanasoff-Berry Computer, ABC). Ennek a prototípusnak az elkészítése és a későbbi kutatás csendben folyt. A gép kettes számrendszert használt. Az adatbevitel lyukkártyákkal történt, az eredményt pedig a gép kártyákra égetett jelek formájában adta meg. Ezt a számítógépet egyenletrendszerek megoldására használták. 
A gép további fejlesztésének 1942-ben a háború vetett véget. Amikor Atanasoff felhívta gépére az IBM figyelmét, azzal utasították vissza, hogy őket soha nem fogják elektronikus számítógépek érdekelni. Mint tudjuk, nem így történt!Colossus
A II. világháború alatt tudósok és matematikusok egy csoportja Angliában létrehozta az első teljesen elektronikus digitális számítógépet, a Colossust. A gép 1943 decemberére készült el és 1500 elektroncsövet tartalmazott. 5 kHz-s órajellel dolgozott, másodpercenként 25.000 karaktert tudott feldolgozni. Összesen tíz darab ilyen gép készült. Rejtjelezett német rádióüzenetek megfejtésére használta sikeresen egy Alan Turing által vezetett csoport (ő ugyanaz a Turing, aki a korábban említett Turing-gépet kitalálta). A németek ENIGMA nevű rejtjelét is ezzel fejtették meg.ENIAC
Ismertté az ABC utóda, az első általános célú elektronikus digitális számítógép, az ENIAC (Electronic Numerical Integrator And Computer) vált. Az ENIAC tervezését a második világháború alatt kezdte el katonai célokra John Presper Mauchly és John William Eckert. A gépet a Pennsylvania egyetemen építették, a munkát 1946-ban fejezték be. Az ENIAC 17.468 elektroncsövet tartalmazott, több mint 100 kW elektromos energiát fogyasztott és 450 m2 helyet foglalt el (több mint 30 m hosszú termet építettek az elhelyezéséhez). A gép tömege 30 tonna volt, megépítése tízmillió dollárba került.
Sokkal gyorsabb volt, mint a relés számítógépek: az összeadást 0,2 ms, a szorzást 3 ms alatt végezte el. A programja azonban fixen be volt “drótozva” a processzorba és csak mintegy kétnapos kézi munkával, villamos csatlakozások átkötésével lehetett megváltoztatni.
A gép memóriája 20 db tízjegyű előjeles decimális számot tudott tárolni. Mindegyik számjegy tárolására 10 db elektroncsövekből épített flip-flop szolgát. Mindegyik flip-flop megfelelt egy-egy számjegynek: egy számjegy tárolásához a neki megfelelő flip-flopot 1-re 
állították, az összes többit 0-ra.
állították, az összes többit 0-ra. Az elektoncsövek megbízhatatlansága miatt a gép csak rövid ideig tudott folyamatosan működni.
Az ENIAC-ot ballisztikai és szélcsatorna-számításokra használták. Egy feladatsor kiszámítása a gépnek 15 másodpercig tartott, ugyanez egy szakképzett embernek asztali kalkulátorral 10 órás munka volt!! A gépet 1956-ban lebontották, mert elavult. Jelenleg egy olcsó zsebszámológép is nagyobb teljesítményű, de az ENIAC technikatörténeti érdemei vitathatatlanok.
Vita folyt arról, hogy melyik az első általános célú elektronikus digitális számítógép. 1973. október 19-én úgy döntött a bíróság, hogy az Atanasoff-Berry Computert illeti meg ez a cím.EDVAC
Az ENIAC utóda, az EDVAC (Electronic Discrete Variable Automatic Calculator) ugyancsak Mauchly és Eckert vezetésével épült 1944-től 1948-ig (véglegesen csak 1951-ben helyezték üzembe). Ez a gép már Neumann János (1903-1957) magyar matematikus elvei alapján úgy készült, hogy a programot és az adatokat a memóriában tárolta.
Az EDVAC sok fontos vonásban különbözött elődeitől. Sokkal nagyobb memóriája volt: egy elsődleges (operatív) tár és egy másodlagos, lassabb, nagyobb kapacitású tár.
Egy program végrehajtásához előbb az egész programot és az adatokat be kellett táplálni a memóriába.
Adatbevitelre egy írógépszerű eszközt, adatkivitelre egy nyomtatót alkalmaztak.
Ez volt az első tárolt programú számítógép. Ettől kezdve már a papírból készült lyukszalag olvasási sebessége nem korlátozta a számítógép sebességét és egy új probléma megoldásához nem kellett a gépet áthuzalozni.
A képen: Neumann János és Robert Oppenheimer az EDVAC előtt.
UNIVAC
Az első kereskedelmi forgalomban is kapható, sorozatban gyártott univerzális számítógép a UNIVAC I. (UNIVersal Automatic Calculator) volt. Ez volt az első számítógép, amely a számok mellett már szöveges információt is tudott kezelni! Többen ezt a gépet tekintik az első generáció igazi kezdetének. A gépet a Remington Rand nevű cég gyártotta. Az ENIAC-hoz és EDVAC-hoz hasonlóan ezt is John Presper Eckert és John Mauchly tervezte.
A gép 5600 elektroncsövet és 18 000 diódát tartalmazott, 19 tonnát nyomott és egymillió dollárba került.
A gép központi része a háttérben látható, az előtérben pedig a vezérlőpult van.
Az első UNIVAC gépet az USA Népességnyilvántartó Hivatala vásárolta meg 1951-ben és mintegy 12 évig napi 24 órás műszakban használta. 1952-ben e gép segítségével jósolták meg az elnökválasztás eredményét még a választás napjának éjszakáján, a szavazatok 7%-ának összeszámlálása után. A UNIVAC I-et először 1954-ben a General Electricsnél alkalmazták üzleti célra. Ebből a gépből összesen 48 darabot gyártottak. A korszak egyéb eredményei
A nyomtatott áramköröket (NYÁK) a második világháború alatt fejlesztette ki az USA-ban a National Institute of Standards and Technology, eredetileg tüzérségi lövedékek gyújtószerkezetében való felhasználásra. Később azonban széles körben elterjedtek, és szinte minden elektronikus eszközben – így a számítógépekben is – ilyen lapra szerelték az alkatrészeket.1950-ben jelennek meg először képernyőn a számítógépes műveletek eredményei az amerikai légiellenőrzési szolgálat egyik félautomata földi állomásán.
1952-ben készül el Moszkvában a MESM és BESZM, az első két szovjet számítógép. [A BESZM (БЭСМ) az első sorozatban gyártott orosz nagy számítógépek (mainframe) típusa. Az elnevezés a Nagy Elektronikus Számítógép (oroszul: Большая Электронно-Счётная Машинa / Bolsaja Elektronno-Szcsotnaja Masina) kezdőbetűiből képzett betűszó.]
1954-ben alkalmaznak először elektronikus számítógépeket üzleti célra (IBM). Ugyanebben az évben jelenik meg az első nagy sorozatban gyártott számítógép, az IBM 650. Összesen 2200 darabot gyártanak belőle. Ennek a gépnek mágnesdobos tára volt, lyukkártyát használtak inputra és outputra.1955 februárjában kezdi az IBM szállítani első kimondottan üzleti számítógépét, az IBM 752-t. Ez a UNIVAC komoly vetélytársának bizonyult: 1956 augusztusára az IBM-nek már 76 installált gépe és 193 megrendelése van, míg a UNIVAC-nak 46 installált gépe és 65 megrendelése. 1956 végére az IBM előnye tovább nő. Az előretörés oka azonban nem a gépek közötti tényleges különbség, hanem az IBM kiváló eladási stratégiája.
2010.04.25. 22:12
Hollerith lyukkártyás adatfeldolgozása
Az Egyesült Államok 1880-as népszámlálásán 55 millió ember adatait gyűjtötték össze.Az adatokat 500 ember összesítette 36 szempont szerint 7 éven keresztül.
Herman Hollerith (1860-1929) német származású amerikai statisztikus ennek láttán találta ki, hogy a Jacquard deszkalapjaihoz hasonló perforált kártyákat adatfeldolgozásra is lehet használni. Így ő volt az első, aki számokat tárolt lyukkártyákkal: egy kártyára egy ember adatait lyukasztotta. Maga a lyukasztás kézi munkával történt.
Az adatok feldolgozására olyan rendszert használt, ahol a lyukkártyák elektromos érintkezők között mentek át. Ahol a kártyán lyuk volt, az áramkör bezárult. Így a lyukakat meg lehetett számolni.
Miután készülékére 1889-ben szabadalmat kapott, ezzel dolgozta fel az USA 1890-es népszámlálási adatait — mindössze négy hét alatt! Ennek sikere láttán alapította 1896-ban a Tabulating Machine Company nevű céget, amelyből aztán 1924-ben megalakult az IBM.A lyukkártyás adatfeldolgozó (tabellázó) gépek használata az 1930-as évek végén vált tömegessé. Egészen az 1960-as évekig használták őket szerte a világon. E gépek működését külső huzalozású vezérlőpanel irányította.
A XX. sz. elejének eredményei
1914-ben Leonardo Torres y Quevedo (1852-1936) olyan programvezérlésű mechanikus számológépeket épített egyedi célokra, amelyeknek kimeneti egysége írógép volt. Tőle származnak a programozási nyelvek első kezdeményezései is.
1932-ben építette Konrad Zuse (1910-1992) Németországban az első mechanikus tárolót tetszőleges adatok tárolására. 
Alan Turing (1912-1954) 1936-ban leírta egy olyan számítógép matematikai modelljét, amely mint a lehető legegyszerűbb univerzális számítógép bármilyen véges matematikai és logikai problémát meg tud oldani. Ez a ma Turing-gép néven ismert eszköz fontos volt a digitális számítógépek kifejlődésében.Leslie Comrie (1893-1950) 1937-ben megalapította Londonban az első kereskedelmi jelleggel működő számítóközpontot. A nagyobb feladatok megoldására több számítógépet és lyukkártyás Hollerith-gépet kapcsolt össze.
Analóg számítógépek a XX. század elején
Analóg számítógépeket a XX. sz. elején kezdtek építeni. A korai modellek tengelyek és fogaskerekek megfelelő mértékben történő elforgatásával számoltak. Ezekkel a gépekkel olyan egyenletek numerikus megoldásait számolták, amelyeket semmiféle más módon nem tudtak megoldani.
1914-ben Udo Knorr a vasút számára elkészítette az első menetrendkészítő diagráfot. A készülék egy-egy vasútvonal mentén kiszámította a menetsebességet és a menetidőt a vasútvonal profiljának, a mozdony típusának és a szállított teher súlyának függvényében. Az eszköz javított változatát Németországban az 1970-es évekig használták.
Mindkét világháborúban használtak bonyolult felépítésű mechanikus, majd később elektromos lőelemképzőket a tengeralattjárókon a torpedók, a repülőkön a bombák célzásához, valamint mozgó célok követésére. Egy másik rendszert a Mississippi tavaszi áradásának előrejelzéséhez használtak.
1930-ban Vannevar Bush és kollégái a Massachusettes Institute of Technology-nél (MIT) elkészítették az első univerzális analóg számítógépet. A készülék 0,1% pontossággal dolgozott és évtizedekig konkurencia nélkül uralta a piacot.
Elektromechanikus (relés) számítógépek
A már említett Konrad Zuse 1936 és 1938 között otthon, szülei lakásának nappalijában épített Z1 néven az első olyan szabadon programozható számítógépet, amely kettes számrendszerben működött. Az adatbevitelre billentyűzet szolgált, az adatkivitel pedig kettes számrendszerben egy világító tábla (fénymátrix) segítségével történt. A számolómű és a tároló telefonrelékből készült. A gép memóriája 16 adat tárolását tette lehetővé. A gép tartalmazott decimális-bináris és bináris-decimális átalakítót is. Ilyen eszközt Zuse készített először.
Az első teljesen működőképes, szabadon programozható, programvezérlésű számítógépet, a Z3-at Zuse 1941-ben fejezte be. Tárolóegység 1600 mechanikus reléből állt, 64 szám tárolására volt képes. A számolómű 400 relé felhasználásával készült. A műveletek jellemző végrehajtási ideje 3 s. Zuse felajánlotta Hitlernek, hogy két év alatt elkészíti a hadsereg számára a gép javított változatát elektroncsövek felhasználásával. Hitler az ajánlatot azzal utasította vissza, hogy még a gép elkészülte előtt meg fogják nyerni a háborút.
Az első teljesen automatikusan működő általános célú digitális számítógépet az Egyesült Államokban, a Harvard egyetemen fejlesztették ki Howard Aiken vezetésével. A tervezéshez az IBM 5 millió dollárral járult hozzá és a gép megépítését is az IBM végezte. 
Ez volt a Mark I.Relékből épült fel, 3304 db kétállású kapcsolót tartalmazott, összesen kb. 760.000 alkatrészből állt és 500 mérföld (800 km) huzalt használtak fel hozzá. A gép kb. 15 m hosszú és 2,4 m magas volt.
A memóriája a mechanikus számológépekhez hasonlóan fogaskerekekkel, tízes számrendszerben tárolta az adatokat, 72 db 23 jegyű számnak volt benne hely. Az adatbevitel lyukkártyákkal történt. A programot lyukszalag tartalmazta, ez vezérelte a gép működését. A szalag végtelenítve volt (hurkot alkotott), így a gép folyamatosan tudta olvasni és emiatt egymásután akárhányszor 
végrehajthatta a szalagon lévő utasítás-sorozatot.
végrehajthatta a szalagon lévő utasítás-sorozatot.A gépnek egy összeadáshoz 0,33, egy szorzáshoz 4, egy osztáshoz 11 másodpercre volt szüksége és gyakran meghibásodott.
A munkát 1939-ben kezdték és 1944-ben készültek el.
A tengeri tüzérség részére készítettek vele lőtáblázatokat. Ezt a számítógépet 1959-ig használták.
Zuse cége 1967-ig gyártott számítógépeket. Az 1956-ban bevezetett (még mindig relés) Z11-ből kb. 50 db készült.
2010.04.25. 21:48
Pascal összeadógépe
Az első, egységes egészként működő összeadógépet Blaise Pascal francia filozófus tervezte 1642-ben.
A gépet fából készítette az akkor csupán 19 éves Pascal, adóbeszedőként dolgozó apja számára, hogy megkönnyítse annak munkáját.
A számológép megmaradt az utókornak. A számokat a gép elején lévő kerekeken kell beállítani, az eredmény pedig a gép tetején lévő kis ablakokban látszik. Ez az eszköz tízfogú fogaskerekeket tartalmaz. A fogaskerekek minden foga egy-egy számjegynek felel meg 0-tól 9-ig. Minden helyiértéknek megfelel egy ilyen fogaskerék (hatjegyű számokat lehet a géppel összeadni). A kerekek úgy kapcsolódnak össze, hogy számokat lehet összeadni vagy kivonni a fogaskerekek megfelelő számú foggal történő elforgatásával: ha a legkisebb helyiérték fogaskerekét egy foggal (36 fokkal) elfordítjuk, az a mozgásiránytól függően 1 hozzáadását vagy levonását jelenti a gépben éppen látható számból. Ebben a gépben így működik a tízes-átvitel: ha az egyik helyiérték kereke a 9-es állásból a 0-ba fordul, akkor a következő nagyobb helyiérték kerekét egy foggal elfordítja.
Leibniz számológépe
Az 1670-es években Gottfried Wilhelm Leibniz (1646-1716) német filozófus és matematikus Pascal gépét továbbfejlesztette. 1672-ben készítette el gépét, amivel már szorozni, osztani és gyököt vonni is lehetett. Ez volt az első olyan számológép, amellyel mind a négy alapműveletet el lehetett végezni. Tulajdonképpen két külön részből állt: az összeadómű Leibniz szerint is megegyezett Pascal megoldásával, a szorzómű tartalmazott új megoldást. A gép nyolcjegyű számokkal való számoláshoz készült, de a tízesátvitel során felmerülő mechanikus problémák miatt sosem működött kielégítően.
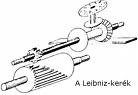A tökéletesítést Pascal gépéhez képest a bordás henger (vagy bordás tengely) alkalmazása jelentette. Az alapelv az ábráról jól leolvasható: a henger felületén 9 db, eltérő hosszúságú borda van, ezek széles fogaskerék-fogként működnek. A hengerhez illeszkedő fogaskerék saját tengelye mentén elmozdítható, és megfelelő beállításával elérhető, hogy a bordás henger egy teljes körülfordulása során fogaiba pontosan 1, 2, ... 9 számú borda akadjon be és így ennyi foggal forduljon el a fogaskerék.
Ha tehát a fogaskerék tengely menti eltolásával beállítják a szorzandót (hogy hány borda akadjon a fogakba), akkor a bordáshengert annyiszor körbeforgatva, amennyi a szorzó, a fogaskerék a két szám szorzatának megfelelő számú foggal fordul el. Ezzel a megoldással elsőként sikerült két szám szorzását és osztását egy tengely megfelelő számú körbeforgatásával megoldania. A bordás henger jelentette egészen a XIX. sz. végéig az egyetlen gyakorlatban is kivitelezhető mechanikus megoldást a szorzás gépesítésére és még e században is alkotórésze maradt az összes mechanikus számológépnek.
Leibniz nevéhez még két olyan elméleti felfedezés is fűződik, aminek szerepe van az informatika fejlődésében. 1666-ban bebizonyította, hogy egy számolási művelet egymás után elvégezhető egyszerűbb lépések sorozatára bontható, 1679-ben pedig ismertette a számítástechnikában alapvető fontosságú kettes számrendszert (bár ennek semmi köze sem volt Leibniz számológépéhez).
1905-ben készítették az első teljesen automatikus, gombnyomásra működő számológépet. A négy alapműveletes számológépeket az 1960-as években használták a legszélesebb körben. A szegedi egyetemen még az 1970-es évek közepén is használták. A felsőbb éves matematikusok numerikus matematika gyakorlataira ilyen mechanikus “kurblis” számológépeket vittek be számolási segédeszköz gyanánt.
Mechanikus számológép az 1960-as évekből
Jacquard automata szövőgépe
Folyamatok vezérlésére már évszázadok óta alkalmaztak különböző vezérlési módokat. Zenegépekben pl. a tüskés henger volt a jellemző megoldás. A henger méret (vagyis hát a kerülete, mert azon voltak a tüskék) természetesen megszabta a program hosszát: a henger minden körülfordulása ugyanazt a tevékenységet idézte elő.
A mintás szövés vezérlésére viszont olyan módszer kellett, amivel egyrészt hosszabb programot is meg lehet adni, másrészt pedig viszonylag egyszerűen lehet a mintát megváltoztatni, a szövőszéket “átprogramozni”. Az idők folyamán többféle ilyen vezérlést találtak fel. Brösel 1690 körül vászonszalagra faelemeket ragasztott, ezzel határozták meg a szőtt anyag mintáját. A mintát a vászonszalagok cseréjével lehetett változtatni. A lyoni selyemszövőgépekben kb. 1725 óta lyukasztott papírcsíkok látták el ugyanezt a feladatot. 
Joseph Marie Jacquard (1752-1834) francia feltaláló a vezérlést tovább tökéletesítette. 1810-ben olyan automatikus szövőszéket tervezett, amelynél fából készült vékony, megfelelően kilyuggatott lapok (“kártyák”) vezérelték a bonyolult minták szövését. A lyukkártyákat láncra fűzte, ezzel lehetővé téve a minták (azaz a szövőszék vezérlésének) gyors és könnyű megváltoztatását. (Ez a “gyors és könnyű” állítólag mintegy 15 napos munkát jelentett.)
Létrejöttek tehát az automaták, amelyek emberi irányításra nem szorulnak, és bizonyos határok között önmagukat irányítják.
A képen a szövőszék tetején látható a lyukkártyás vezérlőszerkezet.
Babbage munkássága
A XIX. században Charles Babbage (1792-1871) brit matematikus és feltaláló kidolgozta a modern digitális számítógép alapelveit.
Őt tekinthetjük a számítástechnika atyjának.
Több új típusú gépet is kigondolt. Ilyen volt a Difference Engine (differenciagép), amit logaritmustáblázatok készítésére tervezett az 1820-as évek elején. A gép a számolás eredményét a tervek szerint pontozóval közvetlenül a nyomda által használható fémlemezbe írta volna. A differenciagép bizonyos függvényértékek (négyzetek, harmadik hatványok, logaritmusok, stb.) sorozatának kiszámítását célozta.
Babbage hat, egymáshoz kapcsolódó számolóművet tervezett, mai ismereteink szerint hibátlanul. A gép 20 jegyű számokkal dolgozott volna. Babbage csak a gép egyes részeit tudta elkészíteni, a munkát azonban nem tudta befejezni: részben anyagi okok miatt, részben pedig a kor technikai lehetőségei nem voltak elegendőek. 1834-ben a differenciagép előállítási költségeit 17 470 fontra becsülték (egy gőzmozdony ugyanekkor 1000 fontba került!!).
Az első működő differenciagépet Babbage készülékének egyszerűsítésével 1853-ban készítette el Pehr Scheutz és fia, Edvard Scheutz. Ez a gép harmadrendű differenciákat és 15 jegyű számokat kezelt csak. Christel Hamann tovább tökéletesítette a berendezést, és segítségével 1910-ben tízjegyű logaritmustáblázatot jelentetett meg. Differenciagépeket egészen az 1940-es évekig használtak matematikai táblázatok készítésére.
A londoni Science Museumban 1991-ben Babbage részletes rajzai alapján megépítették az eredeti differenciagép egyszerűsített változatát korszerű anyagokból. A gép négyezer alkatrészből áll, méretei is tekintélyesek:
3,4 m × 0,5 m × 2,1 m.
A berendezés tökéletesen működött: hibátlanul kiszámította a 7. hatványok táblázatának első száz értékét.
1833-ban a differenciagép elveinek továbbfejlesztésével tervezte meg Babbage az Analytical Engine-t (analitikus gépet). A gép elkészítéséhez a kormánytól kapott előlegként 17 000 font támogatást, de a saját tőkéjéből is ráköltött mintegy 20 000 fontot (más forrás szerint a támogatást nem az analitikus géphez, hanem a differenciagéphez kapta Babbage). A kormány 1842-ben, miután még mindig nem voltak látható eredmények, megvonta támogatását Babbage munkájától. (“Mi lenne, ha a gépet arra használnánk, hogy számolja ki, mikor fog működni?” — élcelődött Robert Peel miniszterelnök.)
Ez a gép teljes egészében sohasem épült meg, pedig a modern számítógépek sok sajátságával rendelkezett.
Babbage univerzális gépet tervezett, amely adatbeviteli és eredmény-kiviteli egységből, számolóműből és részeredmény-tárolóból állt volna.
A gép lyukkártyákról olvasta volna be az információkat, tudott volna utasításokat és adatokat tárolni, matematikai műveleteket végrehajtani és adatokat kinyomtatni.
Lyukkártyák vezérelték volna a tulajdonképpeni számítási folyamatokat is. Megjelent a feltételes vezérlésátadás ötlete: egy szám előjelének függvényében a gép kétféleképpen folytatta volna működését.
A tárolómű 200 részeredmény tárolására lett volna alkalmas. Erre a célra 1000 db, egyenként 50 fogaskereket tartalmazó oszlopot tervezett Babbage.
Haláláig ezen a gépen dolgozott, bár az építése már kezdetben megakadt: a kor finommechanikai lehetőségeivel ezt a gépet nem lehetett elkészíteni. Ha megépült volna, egy futballpálya területét foglalta volna el és öt gőzgép energiája kellett volna a működtetéséhez.
A gép működési elvei miatt azonban sok történész Babbage-et és a munkatársát, Augusta Ada Byron (Augusta Ada Lovelace) matematikust (Lord Byron angol költő lányát) tartja a modern digitális számítógép igazi feltalálójának.
Egy olasz mérnök írt francia nyelvű beszámolót Babbage differenciagépéről. Ezt olvasta az akkor 27 éves Augusta Ada Lovelace. Ő javasolta Babbage-nak, hogy ne decimális, hanem bináris formában tárolja a számokat. Ugyancsak ő találta ki, hogy hogyan lehetne a géppel egy utasítás-sorozatot többször végrehajtatni. Ada Lovelace-ről nevezték el később az Ada programnyelvet.
2010.04.17. 20:04
A számoláshoz az első segédeszközt a kéz ujjai jelentették. Ezért volt “kézenfekvő” a tízes számrendszer használata. Később köveket, fadarabkákat is használtak a számolás segítésére alkalmi eszközként.
Ezután jelentek meg a már kimondottan számolás céljára készített, megmunkált, tartós használatra szánt kövek és pálcikák. A számolópálcák használatának az i.e. V. sz.-ból is van nyoma Kínában. Koreában még a XX. sz. elején is ilyen pálcikákkal tanították a gyerekeket számolni. Az ábrán látható régi kínai ún. pálcikaszámjegyek világosan magukon viselik a számolópálcák használatának nyomát.
Az abakusz
Az abakusz ókori (valószínűleg mezopotámiai) eredetű egyszerű számolási segédeszköz. Rudakon, drótokon vagy hornyokban ide-oda mozgatható golyókat tartalmaz. Az egy-egy rúdon lévő golyók helyzete egy-egy számjegyet, a rudak egy-egy helyiértéket jelentenek. Így egy hatsoros (hat rudat tartalmazó) abakuszon a legnagyobb ábrázolható szám a 999 999. Az összeadás és a kivonás igen egyszerűen és gyorsan elvégezhető abakusszal, a szorzás és az osztás sokkal körülményesebb. Az abakusznak igen nagy előnye, hogy az analfabéták is tudtak vele számolni!!
A vonalak jelentették az 1-es, 10-es, 100-as, stb. helyiértékeket, a köztük lévő hézag pedig az 5-öt, 50-et, 500-at, stb. A számokat kavicsokból rakták ki, mindegyik helyiértékre a megfelelő számú kavicsot. Használtak ilyen célra porral borított táblát is.
Ezt a fajta vonalas abakuszt használták szerte Európában a római számokkal való számolás idején. Az eredményt igen könnyű volt leírni római számokkal. A későbbi időkben is előfordul, elsősorban a kevésbé képzett emberek körében (éppen ezért “paraszt számvetésnek” is nevezték).
A görögök, perzsák, rómaiak már állandó eszközt, bevésett vonalakat vagy csatornákat tartalmazó táblákat és ugyancsak állandó, a táblához illó méretű köveket használtak a számoláshoz. A kavics latin neve calculus. Ugye nem nehéz ráismerni kalkulátor szó ősére?
A vonalak jelentették az 1-es, 10-es, 100-as, stb. helyiértékeket, a köztük lévő hézag pedig az 5-öt, 50-et, 500-at, stb. A számokat kavicsokból rakták ki, mindegyik helyiértékre a megfelelő számú kavicsot. Használtak ilyen célra porral borított táblát is.
Ezt a fajta vonalas abakuszt használták szerte Európában a római számokkal való számolás idején. Az eredményt igen könnyű volt leírni római számokkal. A későbbi időkben is előfordul, elsősorban a kevésbé képzett emberek körében (éppen ezért “paraszt számvetésnek” is nevezték).
A görögök, perzsák, rómaiak már állandó eszközt, bevésett vonalakat vagy csatornákat tartalmazó táblákat és ugyancsak állandó, a táblához illó méretű köveket használtak a számoláshoz. A kavics latin neve calculus. Ugye nem nehéz ráismerni kalkulátor szó ősére?
Nem szabad lebecsülni az abakusz hatékonyságát. 1946 november 12-én mérte össze erejét a japán Macuzaki, aki szorobánt használt, és az amerikai Wood, aki elektromechanikus számológéppel dolgozott. Azonos számolási feladatokat kellett megoldaniuk. Mindegyik feladatot Macuzaki oldatta meg rövidebb idő alatt!
Néhány kép különböző abakuszokról:
Néhány kép különböző abakuszokról: A Püthagorasz-féle számolótábla
Az ókori Görögországban alakult ki. A gyakran szükséges számítások eredményét egy-egy táblázatba foglalta, az eredményt erről csak egyszerűen leolvasták. Ezek a számolótáblák a matematikai táblázatok ősének tekinthetők.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |
3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | |
4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | |
5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | |
7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | |
8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | |
9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | |
10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |
Az ábra egy ilyen szorzótáblát mutat. A felső soron az egyik szorzótényezőt kell kikeresni, az első oszlopon pedig a másikat. A szorzat a kiválasztott sor és oszlop metszéspontjában leolvasható: az ábrán a 7·8=56 szorzás elvégzése látható.
Schikard számológépe
1623-ban Wilhelm Schikard (1592-1635) tübingeni professzor a négy alapművelet elvégzésére alkalmas számológépet készített. A gép elkészítésére a késztetést valószínűleg a Keplerrel folytatott beszélgetései jelentették. A gépről is csak Kepler iratai között maradt egy vázlat. Az eredeti gép a harmincéves háborúban eltűnt, a Kepler számára készített másodpéldány még a műhelyben elégett, Schikard pedig egész családjával együtt meghalt pestisben, mielőtt még egyet készíthetett volna.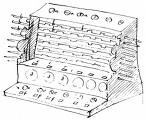 
A vázlat alapján 1960-ban sikerült egy jól működő rekonstrukciót készíteni. A számológép felső része hat darab függőlegesen elrendezett, hengeres pálcát tartalmaz, így legfeljebb hatjegyű számokkal való műveletvégzésre alkalmas. Az egyes számjegyeket a pálcák megfelelő elforgatásával lehet beállítani. A pálcák alatt fogaskerekekből készített számlálómű található. A felhasználónak a pálcákról leolvasott részeredményeket kézzel kellett bevinni a számlálóműbe és azzal összeadni. A végeredmény a gép alján lévő kis nyílásokban jelent meg. Schikard külön számtárcsákat is felszerelt a gépre, amelyek megfelelő elforgatásával a legfeljebb hatjegyű részeredményeket lehetett tárolni, megkímélve ezáltal a felhasználót a leírástól. A gép jelezte a túlcsordulást is: ha a hetedik helyiértékre is szükség lett volna, megszólalt egy csengő.
2010.04.17. 19:25
A számolás (dolgok megszámlálása), a számfogalom már a kőkorszaki ősember által ismert dolog volt. Hogy ez hogyan működött, arra részben a nyelvészet eszközeivel lehet következtetni, részben pedig a felfedezők által a primitív népeknél talált állapotokkal. Mindkét forrás szerint kezdetben csak az egy, a kettő és a sok között tettek különbséget. Később alakult ki a többi szám fogalma. Meg lehet találni a nyomait az ötös (Dél-Amerika), hatos (Északnyugat-Afrika, finnugor népek), hetes (héberek, ugorok), tizenkettes (germán nyelvek), húszas (maják, kelták), hatvanas (Babilon) számrendszernek, illetve ezek keverékeinek is. A jól ismert római számokat a tízes és az ötös számrendszer keverékének tekinthetjük.
A számok rögzítésének ősi módja a megfelelő számú rovás készítése fadarabba, csontba. Már a kőkorszakból fennmaradtak ilyen rovásos csontok. A számok tárolására használtak még csomóba rakott köveket, fadarabokat, zsinegre kötött csomókat is.
A nagy folyó menti kultúrák (Egyiptom, Mezopotámia, az Indus és a Sárga folyó völgye) kialakulása az időszámításunk előtti ötödik évezredben kezdődött. Itt rabszolgatartó államok jöttek létre, fejlett városi élettel, közigazgatással, társadalmi rétegződéssel. Volt kincstár és adó. Számolni kellett, mégpedig elég nagy mennyiségeket is kellett használni és rögzíteni kellett azokat. Az írás már a III. évezred elején ismert volt. A számok leírása, illetve az erre szolgáló külön jelek, a számjegyek kialakulása az írással egy időben történt.
.jpg)
EgyiptomAz egyiptomi matematikai ismeretekről szóló tudásunk egyik forrása a Rhind-papirusz. Feltehetőleg i.e. 1700 körül keletkezett, de a benne szereplő ismeretek minden valószínűség szerint sokkal régebbiek. A képen az egyiptomi matematika néhány jellegzetessége követhető nyomon.
Az egyiptomiak tízes számrendszert használtak. Külön számjegyük volt tíz minden hatványának jelölésére, tehát 1-re, 10-re, 100-ra, stb. (lásd az ábrát). Az ábra alapján azt is nyilvánvaló, hogy milliós nagyságrendű számokkal is dolgoztak. Az írás jobbról balra történt és először a nagy helyiértékeket írták le, tehát ezek a számok jobb végén találhatók.
Ismerték a közönséges törteket. Ezek előállításában az egész számok reciprok értékei, (tehát az 1 számlálójú törtek) fontos szerepet játszottak. Táblázataik voltak arra, hogy az egyéb törteket hogy lehet ilyen reciprokok összegeként előállítani.
Az egyiptomiak tudtak szorozni és osztani is.
Babilon
A babiloniak két legnagyobb, máig élő hozzájárulása a matematikához a 60-as számrendszer és a helyiérték bevezetése. Nádpálcával puha agyagtáblákba írtak, majd azt kiégették. A pálca alakja okozza az ékírás jellegzetes formáját.
A babiloniak is az első kilenc számjegyet megfelelő számú vonással jelölték. A 10-re külön jelük volt, annak ismétlésével írták le a 20-at, 30-at, 40-et és 50-et (lásd az ábrát). A 60 jelölésére újból az 1-es jelét használták (helyiérték!). Így tehát 60-as számrendszerben dolgoztak, de nem volt 60 különböző számjegyük, ahogy azt az ember elsőre elvárná. Nem használták a nullát, így aztán leírva pl. az 1 és a 60 ugyanúgy nézett ki. Csak a szövegkörnyezetből lehetett következtetni rá, hogy pontosan melyikről van szó.
Az 1-nél kisebb helyiértékeket is használták, “hatvanados” törteket írtak.
A hatvanas számrendszer és a helyiértékes számábrázolás aztán elkerült Alexandriába, ahol Ptolemaiosz is ezt használta. Ő már a nulla jelölésére üres helyet hagyott ki a számok leírásakor, de a nulla mint számjegy még nem jelent meg. Ehhez a hindu kultúra kellett.
A római számok
A római számírás eredete nem tisztázott. A kis értékű számjegyek akár a rovásfák utódainak is tekinthetők. Valószínűnek látszik az etruszk eredet is. Nem az általunk is ismert formájuk volt mindig a számjegyeknek.
Például változatok az 1000-es számjegyre: 
A nagy számok írására is voltak jeleik a rómaiaknak, bár ezek nem váltak egységessé. A számok leírásában a kivonásos mód nem volt általános, pl. a 400 előfordul az általunk is ismert CD alakban, de a CCCC alakban is.
A nagy számok írására is voltak jeleik a rómaiaknak, bár ezek nem váltak egységessé. A számok leírásában a kivonásos mód nem volt általános, pl. a 400 előfordul az általunk is ismert CD alakban, de a CCCC alakban is.
Alfabetikus számírások
Több nép is használta azt a módszert a számok írására, hogy az ábécéjük egyes betűihez rendeltek számértéket: az első betű lett az 1 jele, a második a 2, és így tovább a kilencedik betűig. A következő betű a 10-et jelentette, az utána lévő a 20-at, és ez így ment egészen 100-ig. A következő betű már 200-at jelentett, a következő 300-at, stb. A zsidóknál, grúzoknál, etiópoknál a mai napig használatos ez a forma. Az ókori görögöknél is ez volt a legfejlettebb számírás. Tőlük viszont az ábécével együtt átvették a szlávok. Náluk a mindennapi életből ugyan kiszorult, de az ortodox vallásos könyvek még mindig ezt a számírást használják.
A hindu matematika hozzájárulása
A hindu matematika virágkorát 200 és 1200 között élte. Legfontosabb érdeme a tízes számrendszer és a helyiérték együttes, letisztult használata és ennek során a nullának, mint számjegynek a bevezetése.
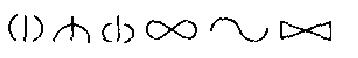
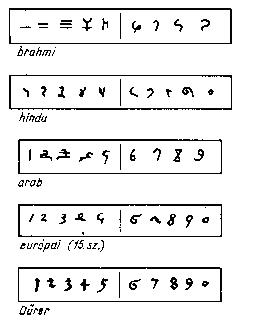
Mai számírási módszerünk egyértelműen innen származik, csak a számjegyek formája változott egy kicsit (lásd az ábrát).
A hinduk a nullát számnak tekintették és a vele való számolás szabályait is megadták. Brahmagupta (598-) megállapította, hogy a nullával való szorzás eredménye nulla; ha egy számhoz nullát adunk vagy nullát vonunk ki belőle, akkor az értéke nem változik; sőt a nullával való osztást is értelmezte oly módon, hogy az így kapott “szám” értéke nem változik, bármilyen számot is adunk hozzá vagy vonunk ki belőle.
A hinduk ismerték a negatív szám fogalmát és a negatív számokra vonatkozó műveleti szabályokat is. Ők vezették be a műveleti jeleket és a zárójelet. A hindu matematika eredményei arab közvetítéssel kerültek Európába.
Európa
Mennyiségek rögzítésére sokáig használták Európa-szerte az úgynevezett rovásfákat. Ezeken már külön jele van az 5-nek, 10-nek, stb. Angliában egészen 1812-ig rováspálcán nyugtázták az adózók által befizetett összeget. A legeltető állattartásban a gazda és a pásztor elszámolása még a múlt század végén is rovásfával történt: tavasszal felvésték a fára a legeltetésre átadott állatok számát, majd a pálcát hosszában kettéhasították. Egyik fele az egyik, másik fele nyugtaként a másik félnél maradt, kizárva így a bármelyikük által elkövetendő hamisítást.
Számolásra Európában igen sokáig a római számokat használták. Gondoljunk bele, hogy hogyan lehet írásban akár csak összeadni is két római számot (bár léteztek a számolást megkönnyítő algoritmusok)! A római számokkal való osztást csak a legnevesebb egyetemeken tanították. A legrégibb európai kézirat, amiben arab számjegyek vannak, a 976-ból származó Codex Vigilianus.
Az ismertetés ellenére nem terjedt el gyorsan az új számírási módszer. Az ellenszenv egyik oka – az újtól való idegenkedésen kívül – az volt, hogy sokkal könnyebben lehetett az üzleti könyveket hamisítani, ha arab számjegyekkel írták: elég volt egy nullát a végére írni, és máris tízszeresére nőtt az ott lévő szám. Sőt, a nullát könnyű volt hatosra vagy kilencesre javítani. Ilyenfajta csalást a római számokkal nem lehet elkövetni. Firenzében 1299-ben rendelettel is megtiltották az arab számok használatát!
A haladást azonban nem lehetett megállítani. Az arab évszámmal ellátott első pénzérmék megjelenési éve néhány országban: Svájc — 1424, Ausztria — 1484, Franciaország — 1485, Németország — 1489, Anglia — 1551, Oroszország — 1654. Az első nyomtatott könyv, amelyben arab számokkal számozták az oldalakat, 1471-ben jelent meg. A közönséges törtekkel való műveletvégzés mai módja a XVII. sz.-ban alakult ki.
A magyarok
A nyelvészek szerint az ősmagyarok először hatos számrendszert használtak. A két, három, négy, öt, hat és száz tőszámneveknek a finnugor nyelvekben közös gyökere van, ekkor ezek a népek még együtt voltak.
Későbbi a hét szó, ez már csak a szűkebb ugor nyelvcsaládra jellemző és a hetes számrendszer használatára mutat. A hetes számrendszerre utal a hétfejű sárkány, a hetedhét ország, a hétpecsétes titok, stb.
A történelmi időkben már tízes számrendszert használtak a magyarok. A legrégibb, a XII. sz.-ból megmaradt ilyen emlék is helyiérték nélküli tízes számrendszer használatára utal. A számok rögzítésére valószínűleg rovásírást használtak. A rovásírás számjegyeinek többfajta változata van, a mellékelt ábra a leggyakoribb formát mutatja. Mivel a megmaradt emlékek több száz évvel a honfoglalás után keletkeztek, feltételezhető, hogy a római számokkal való hasonlóság nem pusztán a véletlen műve.
A legrégibb magyar arab számjegyes emlék 1407-ből származik. Arra is van példa a XV. sz. elejéről, hogy az arab és a római számjegyeket vegyesen használták.
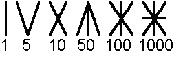
szttort.blog.hu/media/file/számírás története.ppt (kattintásra lép tovább!)
2010.04.17. 17:29