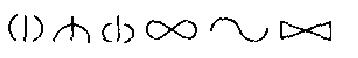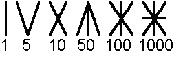A számolás (dolgok megszámlálása), a számfogalom már a kőkorszaki ősember által ismert dolog volt. Hogy ez hogyan működött, arra részben a nyelvészet eszközeivel lehet következtetni, részben pedig a felfedezők által a primitív népeknél talált állapotokkal. Mindkét forrás szerint kezdetben csak az egy, a kettő és a sok között tettek különbséget. Később alakult ki a többi szám fogalma. Meg lehet találni a nyomait az ötös (Dél-Amerika), hatos (Északnyugat-Afrika, finnugor népek), hetes (héberek, ugorok), tizenkettes (germán nyelvek), húszas (maják, kelták), hatvanas (Babilon) számrendszernek, illetve ezek keverékeinek is. A jól ismert római számokat a tízes és az ötös számrendszer keverékének tekinthetjük.

    A számok rögzítésének ősi módja a megfelelő számú rovás készítése fadarabba, csontba. Már a kőkorszakból fennmaradtak ilyen rovásos csontok. A számok tárolására használtak még csomóba rakott köveket, fadarabokat, zsinegre kötött csomókat is.

    A nagy folyó menti kultúrák (Egyiptom, Mezopotámia, az Indus és a Sárga folyó völgye) kialakulása az időszámításunk előtti ötödik évezredben kezdődött. Itt rabszolgatartó államok jöttek létre, fejlett városi élettel, közigazgatással, társa­dalmi rétegződéssel. Volt kincstár és adó. Számolni kellett, mégpedig elég nagy mennyiségeket is kellett használni és rögzíteni kellett azokat. Az írás már a III. évezred elején ismert volt. A számok leírása, illetve az erre szolgáló külön jelek, a számjegyek kialakulása az írással egy időben történt.

Egyiptom

A babiloniak két legnagyobb, máig élő hozzájárulása a matemati­kához a 60-as számrendszer és a helyiérték bevezetése. Nádpálcával puha agyagtáblákba írtak, majd azt kiégették. A pálca alakja okozza az ékírás jellegzetes formáját.
    A babiloniak is az első kilenc számjegyet megfelelő számú vonással jelölték. A 10-re külön jelük volt, annak ismétlésével írták le a 20-at, 30-at, 40-et és 50-et (lásd az ábrát). A 60 jelölésére újból az 1-es jelét használták (helyiérték!). Így tehát 60-as szám­rendszerben dolgoztak, de nem volt 60 különböző számjegyük, ahogy azt az ember elsőre elvárná.  Nem használták a nullát, így aztán leírva pl. az 1 és a 60 ugyanúgy nézett ki. Csak a szövegkörnyezetből lehetett következtetni rá, hogy pontosan melyikről van szó.
    Az 1-nél kisebb helyiértékeket is használták, “hatvanados” törteket írtak.
A hatvanas számrendszer és a helyiértékes számábrázolás aztán elkerült Alexandriába, ahol Ptolemaiosz is ezt használta. Ő már a nulla jelölésére üres helyet hagyott ki a számok leírásakor, de a nulla mint számjegy még nem jelent meg. Ehhez a hindu kultúra kellett.

 

 

 

A római számok

A római számírás eredete nem tisztázott. A kis értékű számjegyek akár a rovásfák utódainak is tekinthetők. Valószínűnek látszik az etruszk eredet is. Nem az általunk is ismert formájuk volt mindig a számjegyeknek.

Például változatok az 1000-es számjegyre: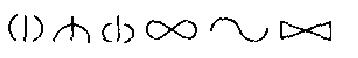




A nagy számok írására is voltak jeleik a rómaiaknak, bár ezek nem váltak egységessé. A számok leírásában a kivonásos mód nem volt általános, pl. a 400 előfordul az általunk is ismert CD alakban, de a CCCC alakban is.

 

 

Alfabetikus számírások

Több nép is használta azt a módszert a számok írására, hogy az ábécéjük egyes betűihez rendeltek számértéket: az első betű lett az 1 jele, a második a 2, és így tovább a kilencedik betűig. A következő betű a 10-et jelentette, az utána lévő a 20-at, és ez így ment egészen 100-ig. A következő betű már 200-at jelentett, a következő 300-at, stb. A zsidóknál, grúzoknál, etiópoknál a mai napig használatos ez a forma. Az ókori görögöknél is ez volt a legfejlettebb számírás. Tőlük viszont az ábécével együtt átvették a szlávok. Náluk a mindennapi életből ugyan kiszorult, de az ortodox vallásos könyvek még mindig ezt a számírást használják.

 

 

A hindu matematika hozzájárulása

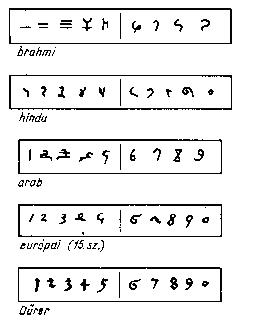A hindu matematika virág­korát 200 és 1200 között élte. Legfontosabb érdeme a tízes számrendszer és a helyiérték együttes, letisztult használata és ennek során a nullának, mint számjegynek a bevezetése. 
    Mai számírási módszerünk egyér­telműen innen származik, csak a számjegyek formája változott egy kicsit (lásd az ábrát).
    A hinduk a nullát számnak tekintették és a vele való számolás szabályait is megadták. Brahmagupta (598-) megállapította, hogy a nullával való szorzás eredménye nulla; ha egy számhoz nullát adunk vagy nullát vonunk ki belőle, akkor az értéke nem változik; sőt a nullával való osztást is értelmezte oly módon, hogy az így kapott “szám” értéke nem változik, bármilyen számot is adunk hozzá vagy vonunk ki belőle. 
    A hinduk ismerték a negatív szám fogalmát és a negatív számokra vonatkozó műveleti szabályokat is. Ők vezették be a műveleti jeleket és a zárójelet. A hindu matematika eredményei arab közvetítéssel kerültek Európába.

 

Európa

Mennyiségek rögzítésére sokáig használták Európa-szerte az úgynevezett rovásfákat. Ezeken már külön jele van az 5-nek, 10-nek, stb. Angliában egészen 1812-ig rováspálcán nyugtázták az adózók által befizetett összeget. A legeltető állattar­tásban a gazda és a pásztor elszámolása még a múlt század végén is rovásfával történt: tavasszal felvésték a fára a legeltetésre átadott állatok számát, majd a pálcát hosszában kettéhasították. Egyik fele az egyik, másik fele nyugtaként a másik félnél maradt, kizárva így a bármelyikük által elkövetendő hamisítást.

Számolásra Európában igen sokáig a római számokat használták. Gondoljunk bele, hogy hogyan lehet írásban akár csak összeadni is két római számot (bár léteztek a számolást megkönnyítő algoritmusok)! A római számokkal való osztást csak a legnevesebb egyetemeken tanították. A legrégibb európai kézirat, amiben arab számjegyek vannak, a 976-ból származó Codex Vigilianus.

Az ismertetés ellenére nem terjedt el gyorsan az új számírási módszer. Az ellenszenv egyik oka – az újtól való idegenkedésen kívül – az volt, hogy sokkal könnyebben lehetett az üzleti könyveket hamisítani, ha arab számjegyekkel írták: elég volt egy nullát a végére írni, és máris tízszeresére nőtt az ott lévő szám. Sőt, a nullát könnyű volt hatosra vagy kilencesre javítani. Ilyenfajta csalást a római számokkal nem lehet elkövetni. Firenzében 1299-ben rendelettel is megtiltották az arab számok használatát!

A haladást azonban nem lehetett megállítani. Az arab évszámmal ellátott első pénzérmék megjelenési éve néhány országban: Svájc — 1424, Ausztria — 1484, Franciaország — 1485, Németország — 1489, Anglia — 1551, Oroszország — 1654. Az első nyomtatott könyv, amelyben arab számokkal számozták az oldalakat, 1471-ben jelent meg. A közönséges törtekkel való műveletvégzés mai módja a XVII. sz.-ban alakult ki.

 

A magyarok

A nyelvészek szerint az ősmagyarok először hatos számrendszert használtak. A két, három, négy, öt, hat és száz tőszámneveknek a finnugor nyelvekben közös gyökere van, ekkor ezek a népek még együtt voltak.

Későbbi a hét szó, ez már csak a szűkebb ugor nyelvcsaládra jellemző és a hetes számrendszer használatára mutat. A hetes számrendszerre utal a hétfejű sárkány, a hetedhét ország, a hétpecsétes titok, stb.

A történelmi időkben már tízes számrendszert használtak a magyarok. A legrégibb, a XII. sz.-ból megmaradt ilyen emlék is helyiérték nélküli tízes számrendszer használatára utal. A számok rögzítésére valószínűleg rovásírást használtak. A rovásírás számjegyeinek többfajta változata van, a mellékelt ábra a leggyakoribb formát mutatja. Mivel a megmaradt emlékek több száz évvel a honfoglalás után keletkeztek, feltételezhető, hogy a római számokkal való hasonlóság nem pusztán a véletlen műve.

A legrégibb magyar arab számjegyes emlék 1407-ből származik. Arra is van példa a XV. sz. elejéről, hogy az arab és a római számjegyeket vegyesen használták.

 

 szttort.blog.hu/media/file/számírás története.ppt (kattintásra lép tovább!)